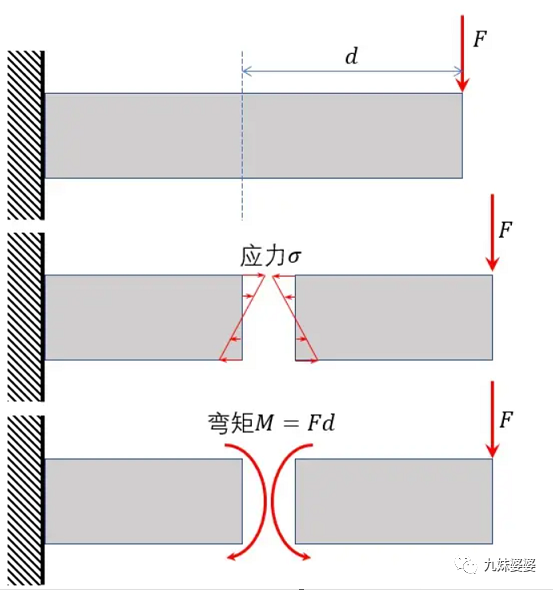
1,、什么是彎矩

我們從最基本的開始,，初中都學(xué)過杠桿原理,，人教版《物理》八年級(jí)下冊(cè)第12章「簡(jiǎn)單機(jī)械」第1節(jié)「杠桿」里就提到過：

「力×力臂」這種計(jì)算方法是初中已經(jīng)講過的,，這其實(shí)就是力矩的計(jì)算,。我們通過這個(gè)物理量來研究物體的旋轉(zhuǎn)，度量產(chǎn)生旋轉(zhuǎn)的作用效果,。力矩越大,，對(duì)旋轉(zhuǎn)產(chǎn)生的影響就越大。

力矩仍然是力產(chǎn)生的,，力是實(shí)際的相互作用,，它的作用效果有平動(dòng)和轉(zhuǎn)動(dòng)兩種。

力對(duì)平動(dòng)的作用效果,，我們用'力的大小'來衡量，力對(duì)轉(zhuǎn)動(dòng)的作用效果，我們用「力矩」來衡量,。

2,、彎矩與剪力的計(jì)算步驟

大學(xué)力學(xué)課程中規(guī)定，彎矩下部受拉為正（上部受壓），上部受拉為負(fù)（下部受壓）,，這是力學(xué)領(lǐng)域的定義,。

但在土木建筑學(xué)領(lǐng)域，為了讓彎曲方向與變形方向一致,，通常上部受壓的梁受到彎矩,，畫在負(fù)方向。在起重機(jī)行業(yè),，通常采用土建領(lǐng)域達(dá)到畫法,，即上部受壓時(shí)，彎矩圖畫在下方,。

畫彎矩圖（或剪力圖）是有技巧的,，或者說快捷途徑的。但各種技巧都是建立在了解結(jié)構(gòu)受力,，對(duì)于各種作用在結(jié)構(gòu)上的荷載使結(jié)構(gòu)產(chǎn)生的反力與內(nèi)力形式都能了然于胸的基礎(chǔ)上,，才會(huì)省略一些相對(duì)來說不是很必要的步驟。

截面法是一種結(jié)構(gòu)力學(xué)中常用的分析方法,，我們還是可以用力矩平衡求得支座反力后利用截面法求得彎矩方程,，根據(jù)彎矩方程繪制彎矩圖，剪力同樣道理,，彎矩和剪力是存在著微分關(guān)系,，對(duì)彎矩求導(dǎo)就是剪力。

（1）由平衡方程計(jì)算支反力,；

（2）選擇截面：截面通常位于結(jié)構(gòu)中的一個(gè)特定位置,，如集中力的附近。

（3）根據(jù)集中力,、集中力偶劃分剪力,、彎矩的變化區(qū)間；

（4）根據(jù)變化區(qū)間建立剪力與彎矩方程,；

（5）繪制剪力圖,、彎矩圖。

3,、集中載荷作用下簡(jiǎn)支梁彎矩和剪力方程推導(dǎo)

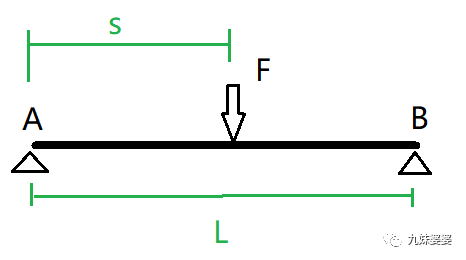
以常見的集中載荷作用下的簡(jiǎn)支梁（起重機(jī)主梁近似為簡(jiǎn)支梁結(jié)構(gòu)）為例,，介紹一下截面法求解彎矩和剪力的過程。

（1）計(jì)算支反力：

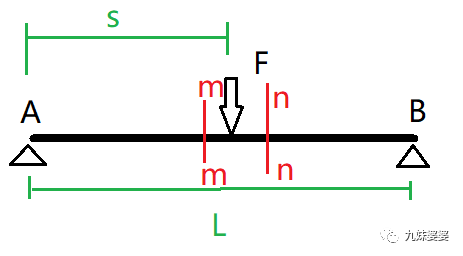
在集中載荷左側(cè)選擇任一截面m-m,；在集中載荷右側(cè)選擇任一截面n-n

設(shè)定截面到支點(diǎn)A的距離為x，根據(jù)截面的位置,，x有兩個(gè)變化區(qū)間：

區(qū)間1：0≤x≤s

區(qū)間2：s≤x≤L

對(duì)截面m-m處,，根據(jù)力的平衡和力矩平衡進(jìn)行分析：

m-m截面處的剪力：FS=FA=F(L-s)/L

m-m截面處的彎矩：M=FAx=F(L-s)x

對(duì)截面n-n處，根據(jù)力的平衡和力矩平衡進(jìn)行分析：

n-n截面處的剪力：FS=FB=Fs/L

n-n截面處的彎矩：M=FAx=F(L-s)x

（5）繪制剪力圖,、彎矩圖

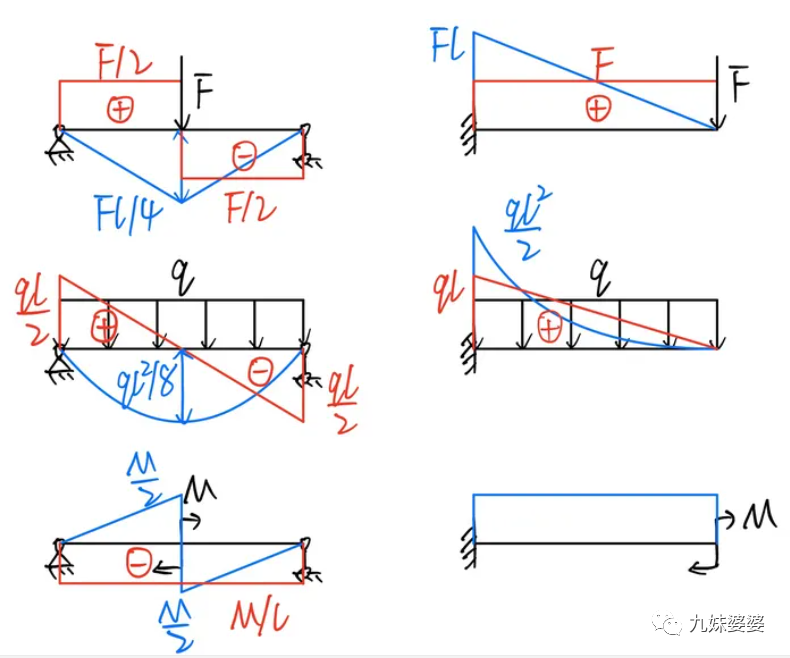
4,、常見的彎矩圖和剪力圖

5,、起重機(jī)械檢驗(yàn)師考題的解析

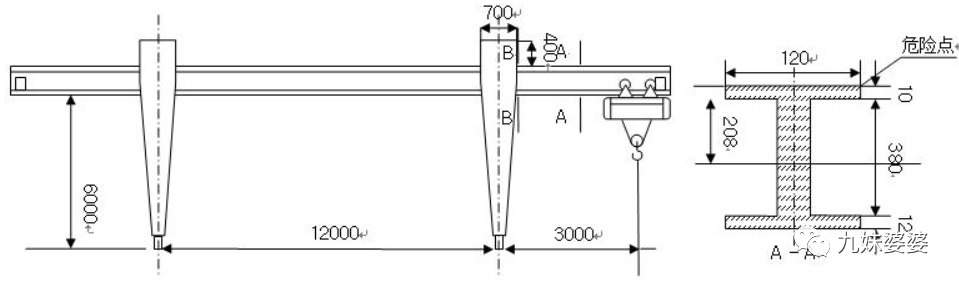
5.1   檢驗(yàn)師考題1

問：（1）畫出滿載葫蘆在跨內(nèi)距左大車輪中心S/4處時(shí),，主梁的彎矩圖和剪力圖（其他問題的解答在隨后幾天給出解析）。

解析：首先說明一點(diǎn),，檢驗(yàn)師考題不會(huì)考大家剪力方程和彎矩方程,，最多考大家能不能畫出來剪力圖和彎矩圖，為了給大家講明白剪力圖和彎矩圖是怎么來的,，我給大家把剪力方程和彎矩方程列出來,。這道題用S表示跨度，和原題保持一致,，注意和前面分析對(duì)應(yīng)起來,。

先把有用信息提出來，集中載荷：
F=（3000+200）×10=32000 N

跨度：S=12 m

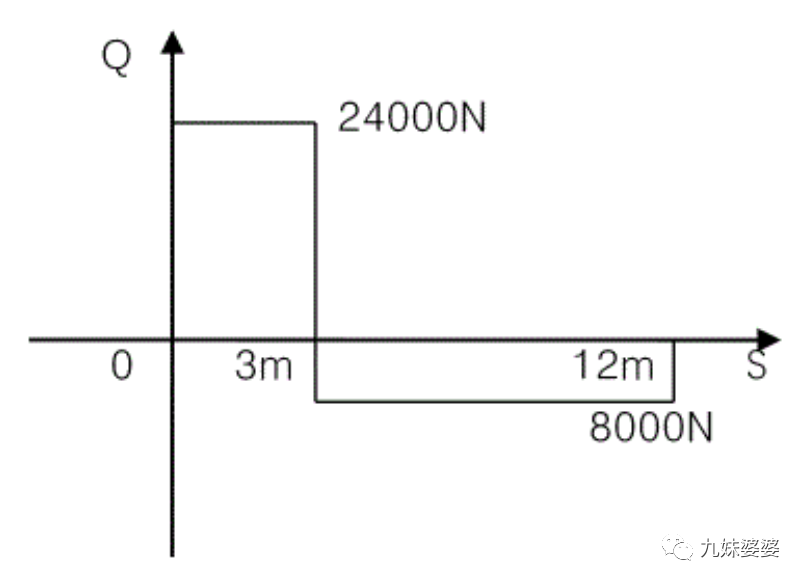
剪力方程：

由剪力方程畫出剪力圖

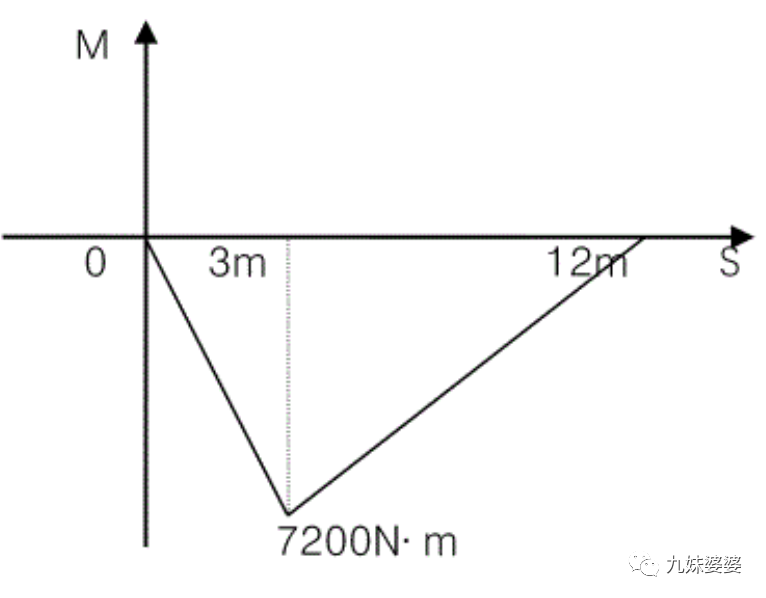
彎矩方程：

由彎矩方程畫出彎矩圖

5.2   檢驗(yàn)師考題2

一型號(hào)規(guī)格為QD32-22.5A5通用橋式起重機(jī)主梁結(jié)構(gòu)如圖所示,，該起重機(jī)技術(shù)資料顯示：薄壁箱形結(jié)構(gòu)主梁,，小車自重為12t,，用吊鉤作業(yè)，整機(jī)采用簡(jiǎn)單控制系統(tǒng)能達(dá)到中等定位精度,，主梁最大截面慣性矩I=1.5×10⁹ mm⁴,，材質(zhì)為Q235,彈性橫量E=2.1×18⁶ N/mm²，g=10 m/s²,，請(qǐng)問：

（1）最大彎矩發(fā)生在主梁什么位置,？計(jì)算主梁最大彎矩值？畫出彎矩圖（其他問題的解答在隨后幾天給出解析）,。

解析：先把有用信息提出來,，集中載荷：

F=（32+12）×10=440 kN

跨度：S=22.5 m

這道題用S表示跨度

由本文第三節(jié)分析，當(dāng)集中載荷作用在跨中,，彎矩最大,。

不過要注意一點(diǎn)，這是通用橋式起重機(jī),，所有的載荷由兩根主梁承擔(dān),，

計(jì)算任一根主梁的彎矩可作為該起重機(jī)的彎矩。

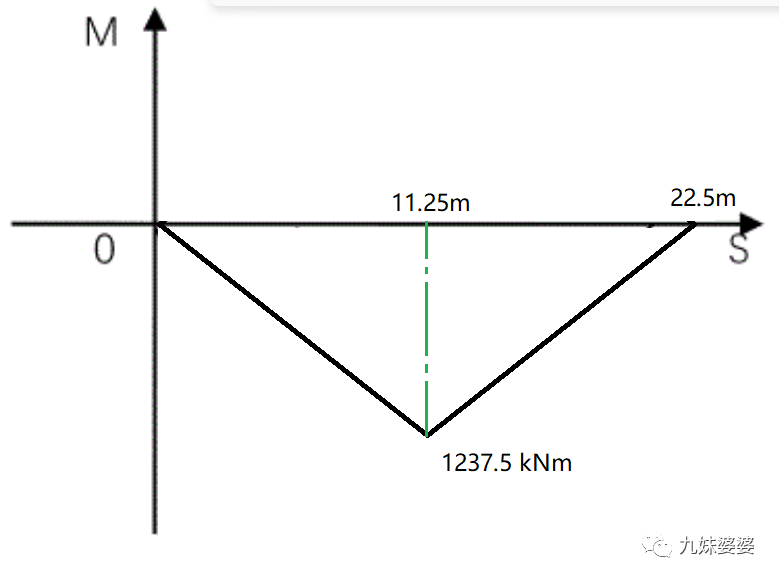
最大的彎矩為：

Mmax=440×22.5/8=1237.5 kNm

如果熟練,，不用再推算彎矩方程,。此時(shí)可以直接畫出彎矩圖。

注意：這道題是一個(gè)錯(cuò)題,，再說的直接一點(diǎn),，2019年之前的起重機(jī)械檢驗(yàn)師考題，所有涉及彈性模量和慣性矩的數(shù)據(jù)全是錯(cuò)的,，是出題組的專家基礎(chǔ)力學(xué)知識(shí)薄弱導(dǎo)致的,。這一點(diǎn)有機(jī)會(huì)在和大家細(xì)談。